math-for-computer-science
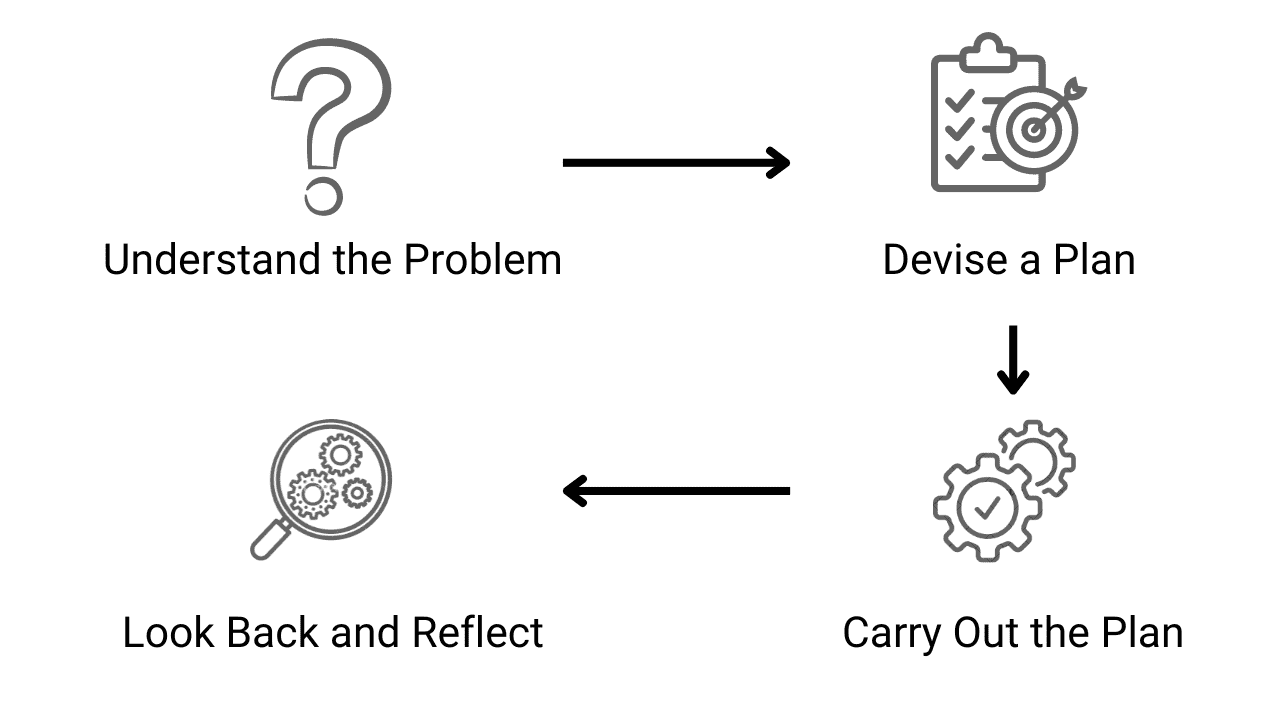
Mathematician George Polya crafted a legacy that has guided countless individuals through the maze of problem-solving. In his book “How To Solve It,” Polya provided four fundamental steps that serve as a compass for handling mathematical challenges.
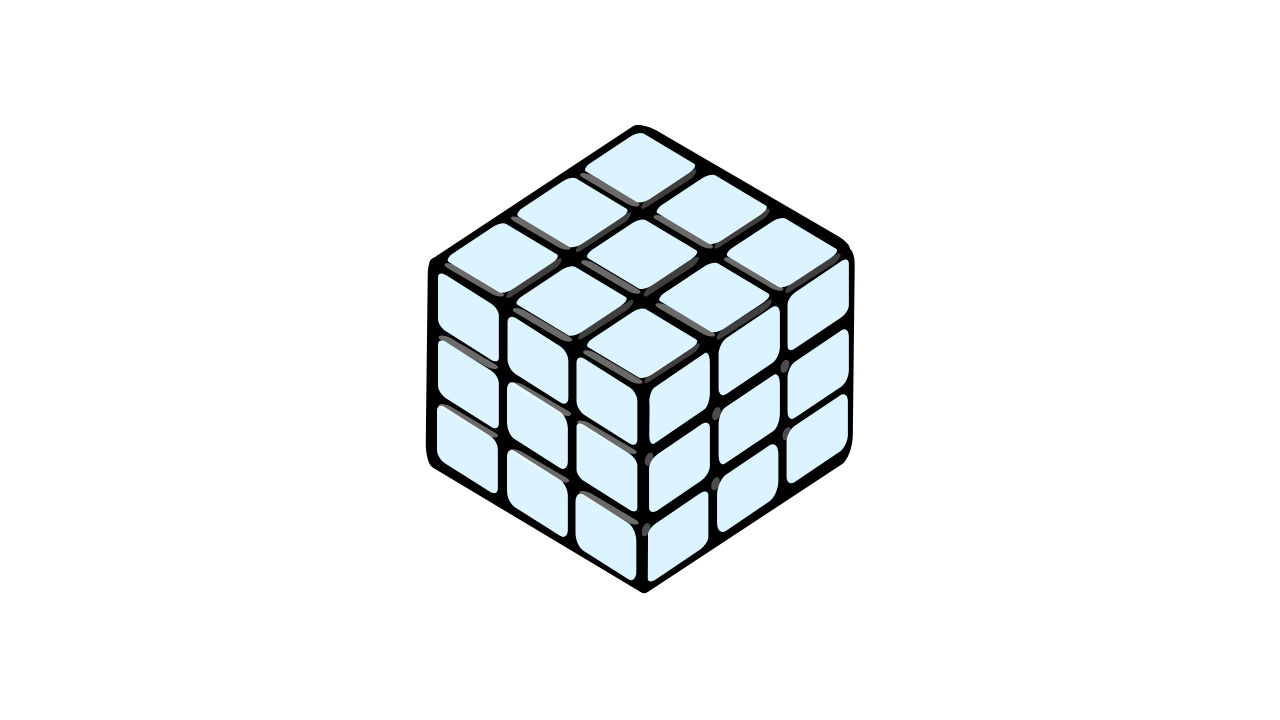
A cube is painted with some color on all faces. Now, we cut it into 1000 small cubes of equal size. How many small cubes are painted?
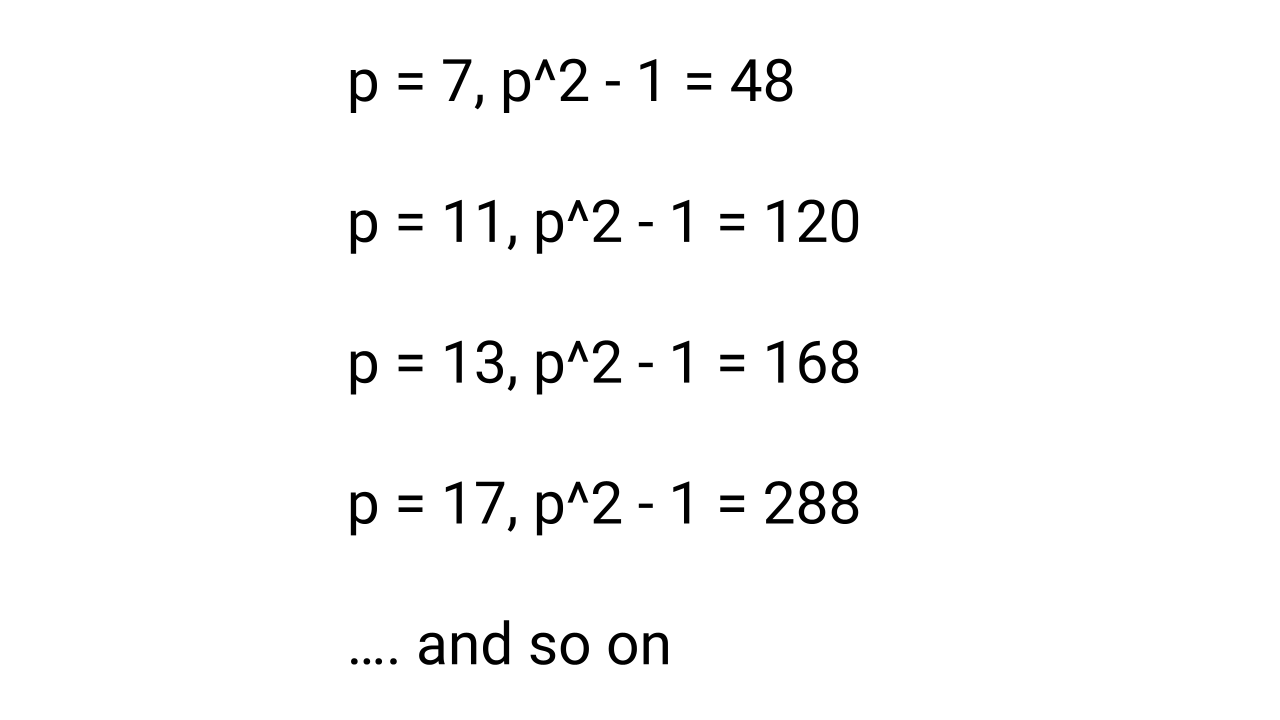
This is one of the basic problems to learn the properties of prime numbers and the divisibility rule. There could be several variations and several ideas of proof available to this question.
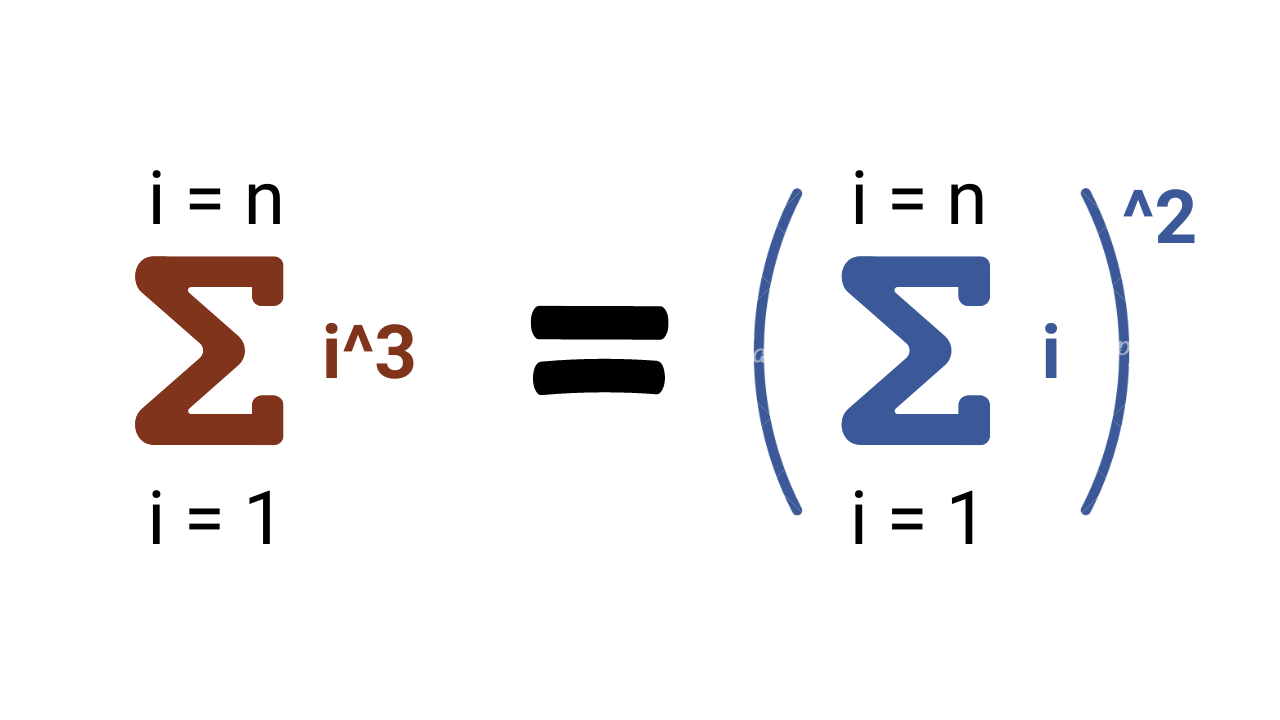
Prove that the sum of the cubes of the first n positive integers is equal to the square of the sum of the first n positive integers.
Just like programming, math is one of the core parts of learning data structures and algorithms. We mainly use math to analyse efficiency of various algorithms. But sometimes, the problem itself contains mathematical property or requires some mathematical insight to find a solution.
The sieve of Eratosthenes is an ancient and efficient algorithm for finding all primes numbers from 2 to n. This algorithm finds all the prime numbers in a segment using O(nloglogn) operations.
Given a positive integer n, write a program to check if the number is prime or not. A number n > 1 is said to be a prime number if 1 and n are its only factors. In other words, a prime number is a number that is divisible only by two numbers itself and one.
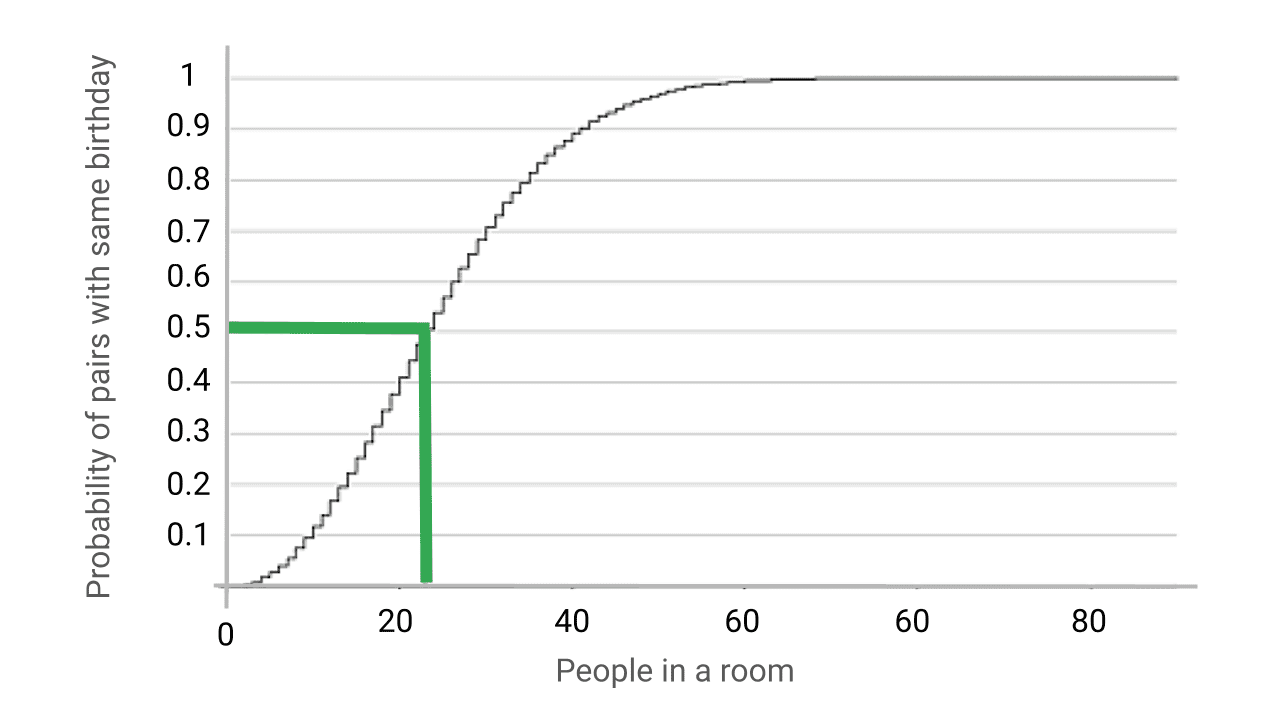
The birthday paradox is strange and counter-intuitive. It's a "paradox" because our brain find it difficult to handle the compounding power of exponents. Real-world applications for this include a cryptographic attack called the "birthday attack".
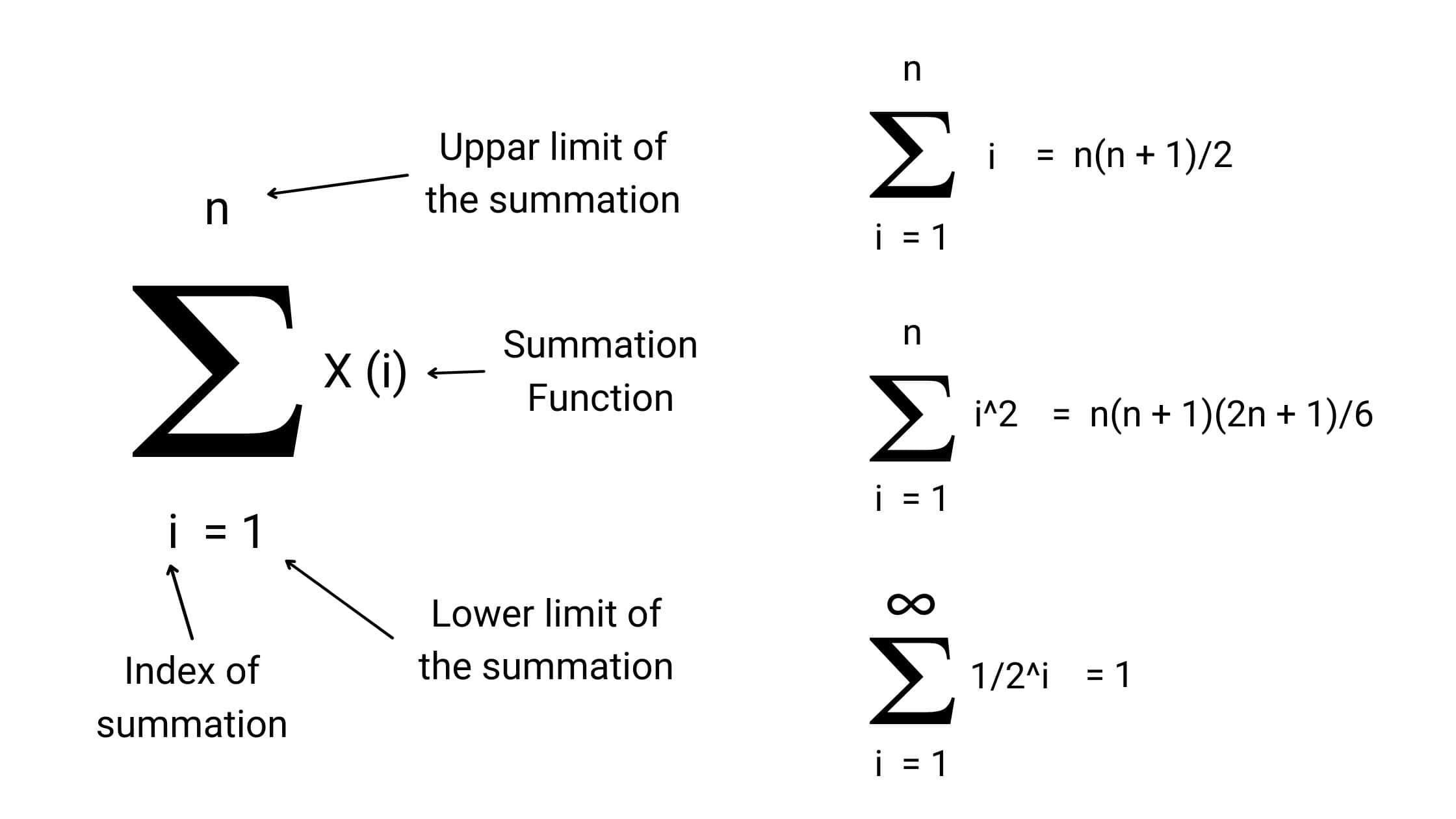
The summation formulas are used to calculate the sum of the sequence. In this blog, we have discussed the visual proofs: the sum of numbers from 1 to n (arithmetic series), the sum of infinite geometric series, the sum of squares of numbers from 1 to n, etc.

Originated from the “Games of Chance,” probability in itself is a branch of mathematics concerned about how likely it is that a proposition is true.
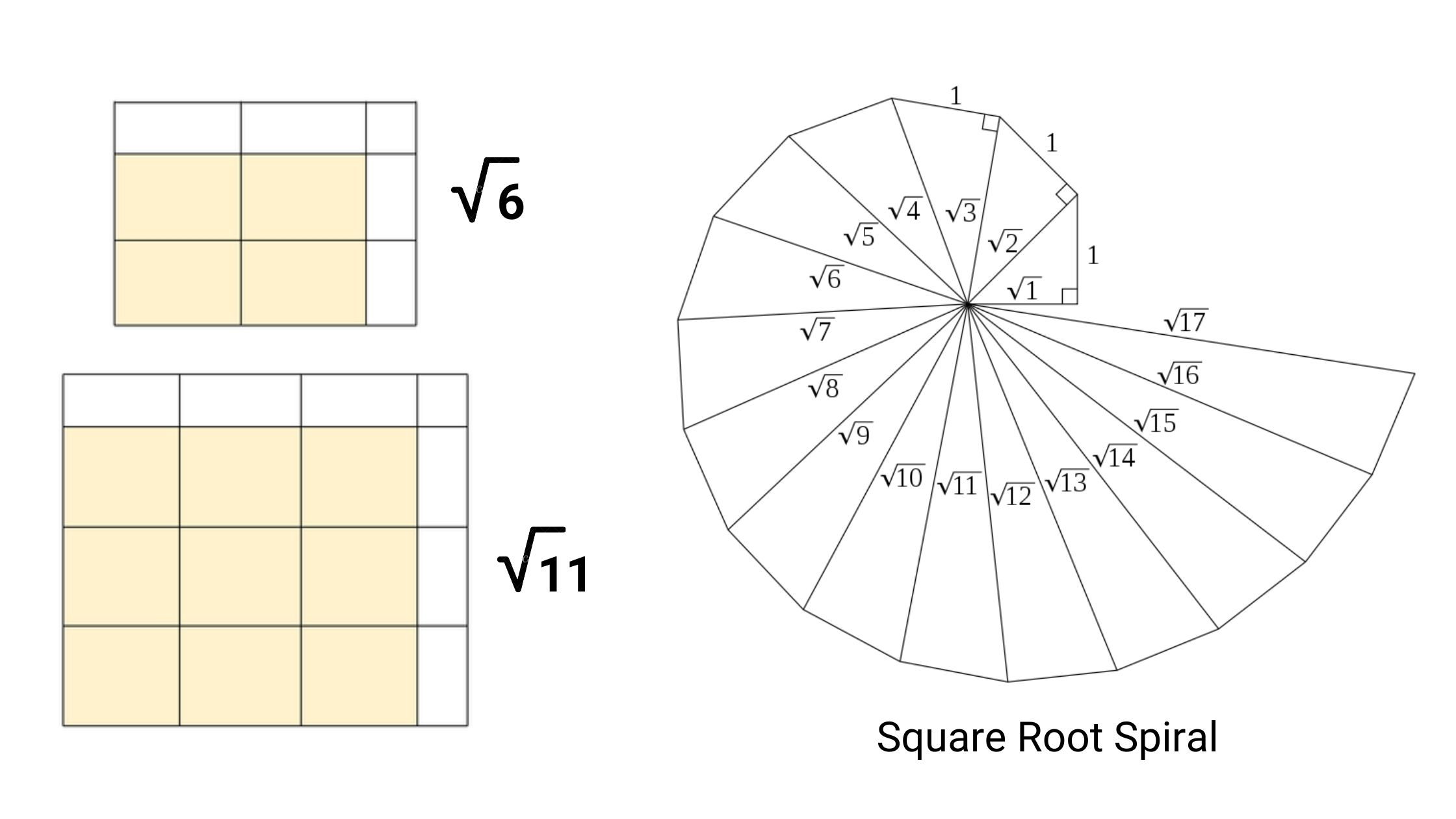
Given a natural number n, find the largest integer less than or equal to √n. This can be seen as a search problem where the search space S is the set {1, . . . , n}, and the number desired is the floor(√n), i.e., the largest integer that is less than or equal to √n.

The Probability distribution lists the probabilities of the events that happened in any given random experiment. For example rolling a dice.

There are 3 doors behind which are two goats and a car. You pick door 1 hoping for the car but don’t open it right away. Monty Hall, the game show host who knows what's behind the doors, opens door 3, which has a goat. Here's the game: do you want to pick door No. 2? Is it to your advantage to switch your choice?

Given two non-negative integers, m and n, we have to find their greatest common divisor or HCF. It is the largest number, a divisor of both m and n. The Euclidean algorithm is one of the oldest and most widely known methods for computing the GCD of two integers.