mathematical-algorithms
Just like programming, math is one of the core parts of learning data structures and algorithms. We mainly use math to analyse efficiency of various algorithms. But sometimes, the problem itself contains mathematical property or requires some mathematical insight to find a solution.
Problem description of the tower of Hanoi: Given a stack of n disks arranged from largest on the bottom to smallest on top placed on a rod A, together with two empty rods B and C. The objective is to move the n disks from rod A to rod C using rod B.
The sieve of Eratosthenes is an ancient and efficient algorithm for finding all primes numbers from 2 to n. This algorithm finds all the prime numbers in a segment using O(nloglogn) operations.
Given a positive integer n, write a program to check if the number is prime or not. A number n > 1 is said to be a prime number if 1 and n are its only factors. In other words, a prime number is a number that is divisible only by two numbers itself and one.
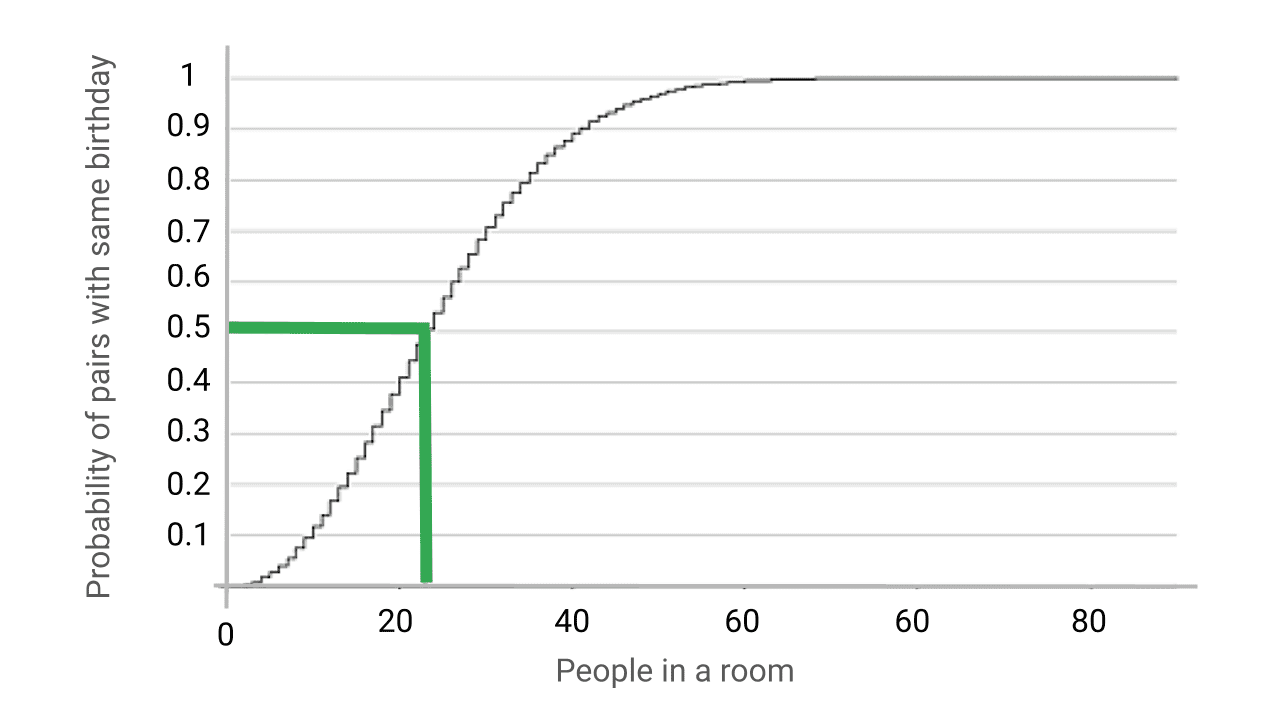
The birthday paradox is strange and counter-intuitive. It's a "paradox" because our brain find it difficult to handle the compounding power of exponents. Real-world applications for this include a cryptographic attack called the "birthday attack".

There are 25 horses among which we need to find out the fastest 3 horses. In each race, only 5 horses can run simultaneously because there are only 5 tracks. What is the minimum number of races required to find the 3 fastest horses without using a stopwatch?
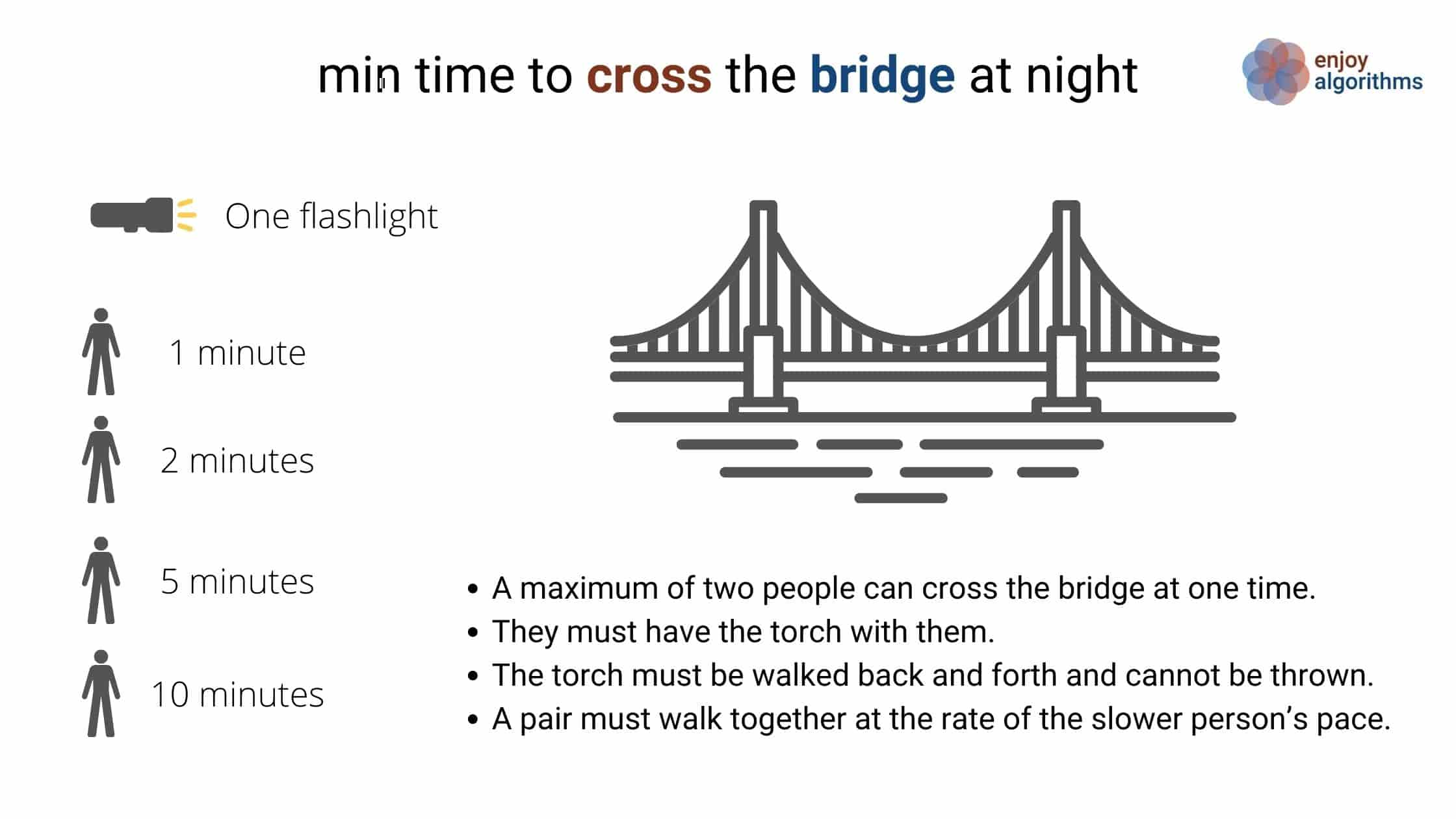
A group of four people, who have one torch, need to cross a bridge at night. A maximum of two people can cross the bridge at one time, and any party that crosses (either one or two people) must have the torch with them. The torch must be walked back and forth and cannot be thrown. Person A takes 1 minute to cross the bridge, person B takes 2 minutes, person C takes 5 minutes, and person D takes 10 minutes. A pair must walk together at the rate of the slower person’s pace. Find the fastest way they can accomplish this task.

There are n+1 people at a party. They might or might not know each other names. There is one celebrity in the group, and the celebrity does not know anyone by their name. However, all the n people know that celebrity by name. You are given the list of people present at the party. And we can ask only one question from each one of them. “Do you know this name”? How many maximum numbers of questions do you need to ask to identify the actual celebrity?
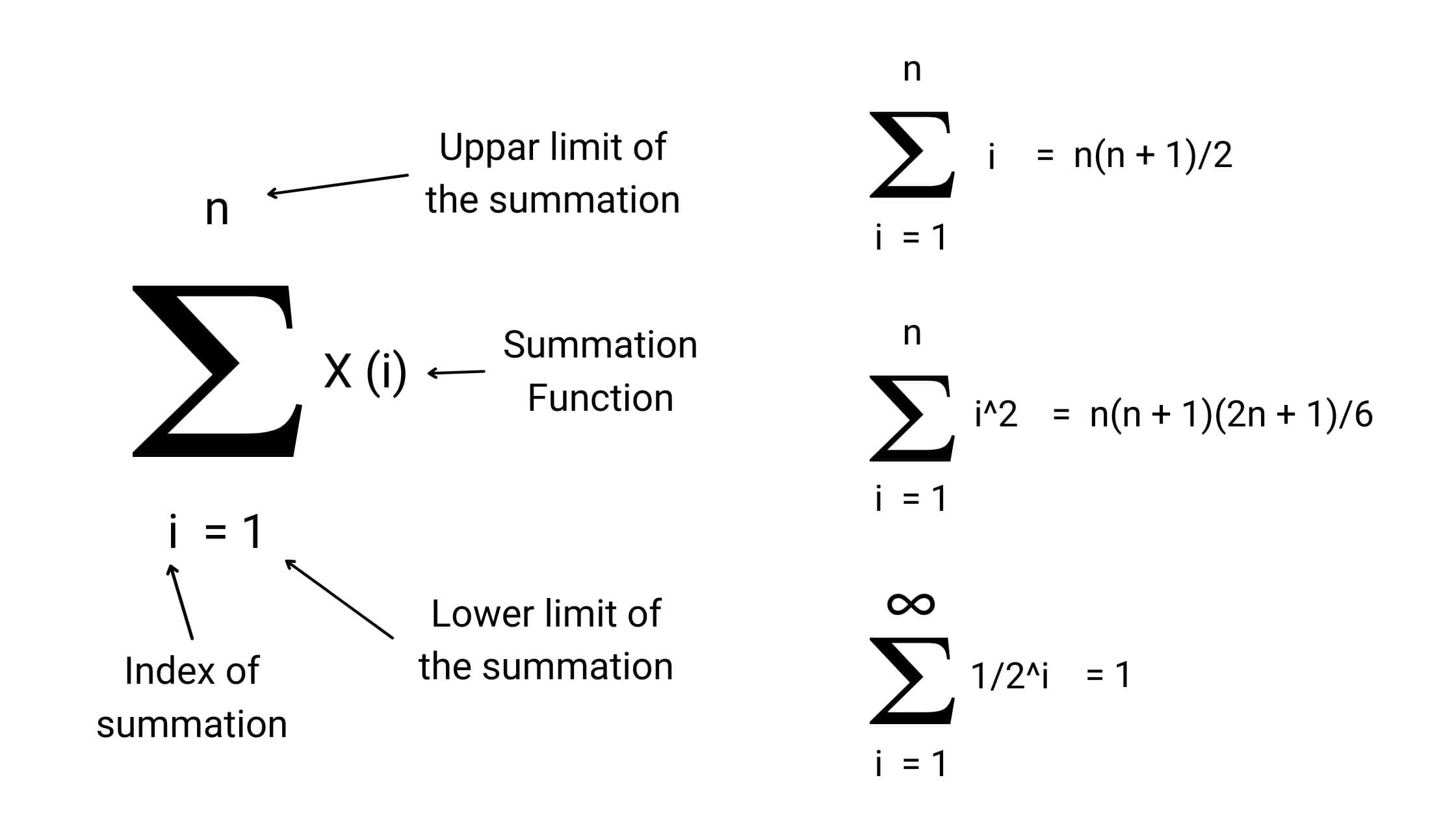
The summation formulas are used to calculate the sum of the sequence. In this blog, we have discussed the visual proofs: the sum of numbers from 1 to n (arithmetic series), the sum of infinite geometric series, the sum of squares of numbers from 1 to n, etc.

You have given n-bulbs connected in a circle with a switch for each bulb. The connection is such that if you change the state of anyone bulb may be on or off, it will toggle the state of its adjacent bulbs. All the bulbs are initially switched off. You have to find the number of steps such that all the bulbs are switched on.

You’ve got someone working for you for seven days and a gold bar to pay him. The gold bar is segmented into seven connected pieces. You must give them a piece of gold at the end of every day. What is the fewest number of cuts to the bar of gold that will allow you to pay him 1/7th each day?

Fill the 3 × 3 tables with nine distinct integers from 1 to 9 so that the sum of the numbers in each row, column, and corner-to-corner diagonal is the same.

Originated from the “Games of Chance,” probability in itself is a branch of mathematics concerned about how likely it is that a proposition is true.
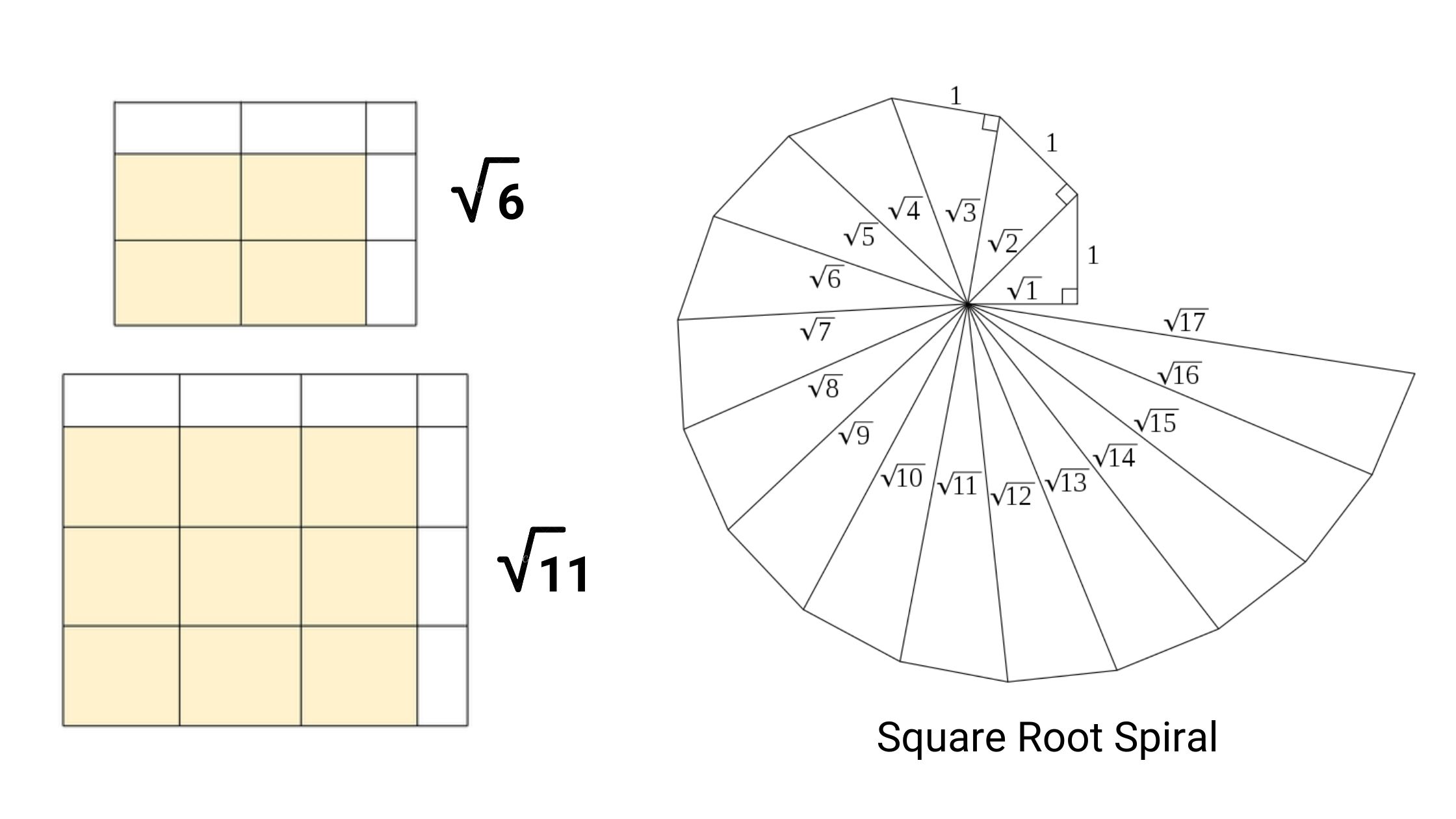
Given a natural number n, find the largest integer less than or equal to √n. This can be seen as a search problem where the search space S is the set {1, . . . , n}, and the number desired is the floor(√n), i.e., the largest integer that is less than or equal to √n.

The Probability distribution lists the probabilities of the events that happened in any given random experiment. For example rolling a dice.
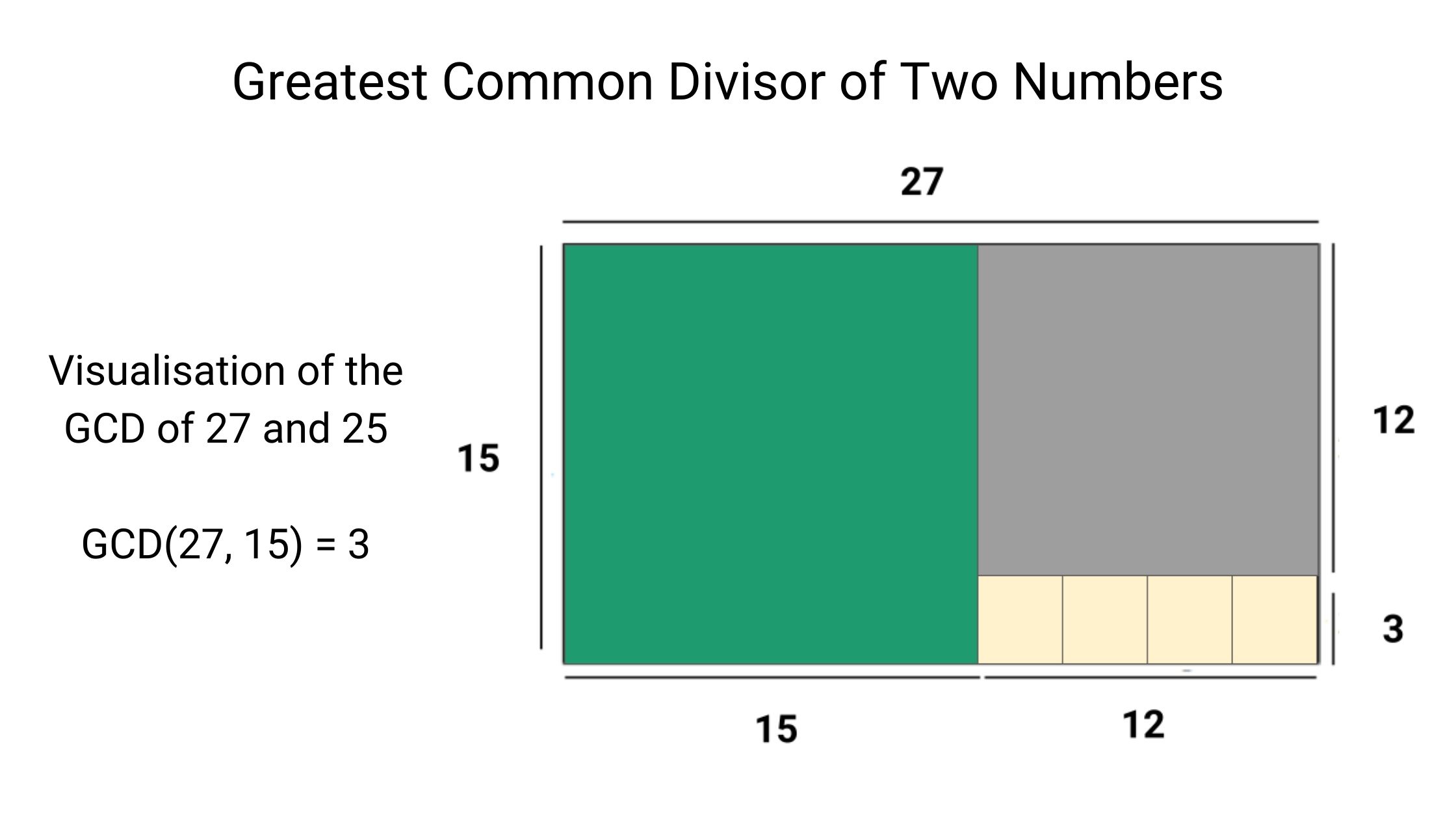
Given two non-negative integers, m and n, we have to find their greatest common divisor or HCF. It is the largest number, a divisor of both m and n. The Euclidean algorithm is one of the oldest and most widely known methods for computing the GCD of two integers.

There are eight identical-looking coins, and one of these coins is fake, which is lighter than genuine coins. What is the minimum number of weighings needed to identify the fake coin with a two-pan balance scale without weights?